A better stepper drive s-curve?

-
One of the not so desirable features of stepper motors is the fact that output torque falls quickly with shaft speed. This is one of the reasons these motors cannot reach high speeds.

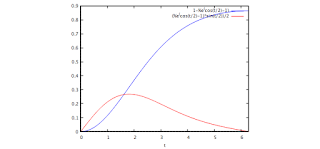
So I was thinking that when we use a s-curve to drive them, instead of choosing a symmetric one, where acceleration is is max in the middle of the acceleration section (as speed raises), I could try one where higher accelerations happen to lower speeds. However, in order to still keep the s-curve shape instead of a sawtooth, I would use the following expression: 1-e^(cos(t/2)-1)and it is shown in blue in the graph.

This will produce a s-curve shape, but modulated with the exponential behavior. Resulting signal will grow faster as the beginning (where more torque is available) and more slowly at the end (where faster speeds are reached and less torque is available).

A first test shows me that, for a bare motor, a faster move can be achieved, more reliably (no missed steps), using this pattern instead of a symmetric sinusoidal s-curve like s(t)=t-sin(t)

 And what is even better is the above is achieved in a relatively shorter time: A 2000-step move would take 94 milliseconds with the exponential-sinusoidal s-curve reliably, while the same move using the symmetric sinusoidal s-curve would take 98 milliseconds but will fail (stall) 20% of the time.

For short movements, the difference may not be great, as no high speeds would be reached, but for high-speed motion, this pattern may be an interesting choice. As you can see, the acceleration is shown in red color in the graph above, and it peaks before 1/3 of the acceleration period.

The video shows how some of the CW movements stall while all the CCW complete without a problem. This is by no means a proof of suitability but just one sample case.


Comments

Post a Comment

Popular posts from this blog

VFD control with Arduino using RS485 link

-
Image
Variable Frequency Drives ( VFD ) allow the control of spindles so speed can accurately be controlled and a detailed acceleration profile for the spindle and reverse rotation can all be handled. In essence a VFD is an three phase inverter for three-phase AC motor. I am using a popular (I mean cheap) Chinese VFD and though the reference manual is not great, I could see there is a built-in RS-485 port. I usually control the start, stop and speed selection using the keyboard on the unit but I thought it will be more useful if I could control everything from the same Arduino is doing our CNC table control. Some cheap RS-485 off eBay and some lines of code later, I can start, stop and change the speed from an Arduino. What a cool thing to have! Some configuration of your VFD are needed before you can use it like that.  You need to set PD163=1 (I am using address 1 in the code). PD=164=1 (for setting serial to 9600bps) and PD165=0 (for using ASCII and 8N1 character for...
Read more

How to get sinusoidal s-curve for a stepper motor

-
Image
After some experimentation, and delving a bit into the math of motion, I realized there can be a significant difference on the motion of a machine by just making small changes. A common and popular approach to smooth one axis of motion is to use a trapezoidal speed pattern, where acceleration and deceleration are uniformly accelerated movements (aka constant acceleration motion) separated by a portion happening at cruising speed. The problem comes with the fact that, while that approach is simple to understand and to code, it does contain sudden changes in the acceleration, that show as spikes on the acceleration derivative, called jerk. These sudden changes in the acceleration translate into undesired vibration in our machines. Most of that can be eliminated by selecting a motion pattern that does not contain sudden changes of acceleration. If we chose a mathematical function for our speed whose second derivative is continuous, then we reduce system vibration quite a lot. One ma...
Read more

Importing OpenSCAD designs into Onshape

-
Image
After using Onshape CAD software for a while I am really fond of it. So one natural thing to do, specially once they have released the Instructor's kit is to start using it in the classroom too. But one thing I was not so sure how to do was to use old designs I made using OpenSCAD. It does not mean I am completely quitting using OpenSCAD but suddenly I can see I can do assemblies in Onshape that will look quite nice for showing and documentation purposes if only I could easily import from OpenSCAD. I am glad to report that the route OpenSCAD --> FreeCAD --> Onshape worked brilliantly. Even more when a few tricks were applied. While some people suggest to import CSG files from OpenSCAD to FreeCAD, I have had more success by directly importing SCAD files into FreeCAD. One trick that worked well for me was to get rid of $fn references, so now circles become real circles (or cylinders) in FreeCAD. If a part keeps some $fn references then your cylinders or circles wi...
Read more